Solve Absolute Value Inequalities
Goal • Solve absolute value inequalities.
Example 1 Solve an absolute value inequality
Solve the inequality. Graph your solution.
a. |x| ≤ 9
b. |x| > 1/4
Solution
a. The distance between x and 0 is less than or equal
to 9. So, -9 ≤ x ≤ 9 . The solutions are all real
numbers less than or equal to 9 and greater than
or equal to -9 .

b. The distance between x and 0 is greater than 1/4.
So, x > 1/4 or x < -1/4. The solutions are all real
numbers greater than
1/4
or less than -1/4.

SOLVING ABSOLUTE VALUE INEQUALITIES
• The inequality |ax + b|< c where c > 0 is equivalent
to the compound inequality -c < ax + b < c.
• The inequality |ax + b|> c where c > 0 is equivalent
to the compound inequality ax + b < -c or ax + b > c.
These statements are also true for inequalities involving
≥ and ≤.
Example 2 Solve an absolute value inequality
Solve |2x - 7|< 9. Graph your solution.
| |2x - 7|< 9 |
Write original inequality. |
| -9 < 2x - 7 < 9 |
Rewrite as compound inequality. |
| -2 < 2x < 16 |
Add 7 to each expression. |
| -1 < x < 8 |
Divide each expression by 2 . |
The solutions are all real numbers greater than -1
and less than 8 . Check several solutions in the original
inequality.
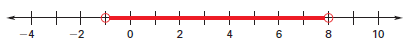
Example 3 Multiple Choice Practice
What is the solution of the inequality |x + 8| - 4 ≥ 2?

Solution
| |x + 8| - 4 ≥ 2 |
Write original
inequality. |
| |x + 8|≥ 6 |
Add 4 to
each side. |
| x + 8 ≥ 6 or x + 8 ≤ -6 |
Rewrite as
compound
inequality. |
| x ≥ -2 or x ≤ -14 |
Subtract 8
from each side. |
The correct answer is D . A B C D
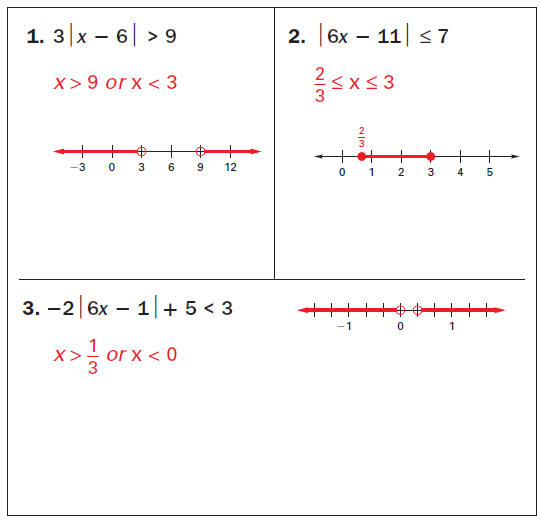
• Guided Practice Solve the inequality. Graph your
solution.
SOLVING INEQUALITIES
One-Step and Multi-Step Inequalities
• Follow the steps for solving an equation, but reverse
the inequality symbol when multiplying or dividing
by a negative number .
Compound Inequalities
• If necessary, rewrite the inequality as two separate
inequalities. Then solve each inequality separately.
Include and or or in the solution.
Absolute Value Inequalities
• If necessary, isolate the absolute value expression on
one side of the inequality. Rewrite the absolute value
inequality as a compound inequality . Then solve
the compound inequality.
|