SOLVING LINEAR EQUATIONS
Definition:
• A linear equation in one variable can be written in the form
ax + b = c
for real numbers a, b, and c, with a ≠ 0.
Important Properties:
• Addition Property of Equality: If a, b, and c are real numbers, then
a = b and a + c = b + c
are equivalent equations. (That is, you can add or subtract the same quantity on
both sides of the
equation without changing the solution.)
• Multiplication Property of Equality: If a, b, and c are real numbers
and c ≠ 0, then
a = b and ac = bc
are equivalent equations. (That is, you can multiply or divide the same nonzero
quantity on both
sides of the equation without changing the solution.)
Common Mistakes to Avoid:
• When clearing the parentheses in an expression like 7-(2x-4), remember that
the minus sign acts
like a factor of -1. After using the distributive property, the sign of every
term in the parentheses
will be changed to give 7 - 2x + 4.
• To clear fractions from an equation, multiply every term on each side by the
lowest common de-
nominator. Remember that 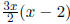 is considered
one term, whereas, is considered
one term, whereas, 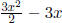 is considered two is considered two
terms. To avoid a mistake, clear all parentheses using the distributive property
before multiplying
every term by the common denominator.
• To preserve the solution to an equation, remember to perform the same
operation on both sides of
the equation.
PROBLEMS
Solve for x in each of the following equations:
|