Solving Quadratic Equations
A quadratic equation is an equation that can be written in
the form
ax2 + bx + c = 0
where a, b, and c are real numbers and a ≠ 0. The solution
to a quadratic equation
is the set of all values that satisfy the equation, i.e. you can replace the
variable with
the value and both sides of the equation will simplify to the same value. There
are
three commonly used methods for solving quadratic equations: factoring, using
the
quadratic equation, and extracting square roots.
• Factoring: This method can be used whenever the
polynomial is factorable.
It is based on the idea that if ab = 0 then either a = 0 or b = 0.
1. By adding and/or subtracting, move all the terms to one
side of the equa-
tion. There should just be a zero left on the other side of the equation.
2. Factor the polynomial completely.
3. Rewrite the equation as two equations, setting each factor equal to zero.
4. Sove both of the resulting equations.
5. Check the answers in the original equation.
Example 1 Solve x2 + 6 = 5x by
factoring.
1. We want to move the 5x to the left-hand side, so we
subtract 5x from both
sides, and we have:
x2 -5x + 6 = 0
2. Factoring the left-hand side, the equation becomes:
(x -3)(x - 2) = 0
3. Setting each factor to zero, we have the two
equations: x - 3 = 0 and
x - 2 = 0.
4. Solving these two equations, we have: x = 3 and x =
2.
5. Checking our answers, we have:
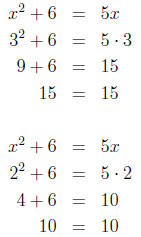
So, the solutions to the equation x2 + 6 = 5x are x = 3 and x = 2.
Example 2 Solve 12 - 5x = 2x2 by
factoring.
1. We want to move the 12 and the ¡5x to the right-hand
side, so that we
can keep the x2 term positive. We subtract 12 and add 5x to both
sides,
and we have:
0 = 2x2 + 5x ¡ 12
2. Factoring the right-hand side, the equation becomes:
0 = (2x - 3)(x + 4)
3. Setting each factor to zero, we have the two
equations: 2x - 3 = 0 and
x + 4 = 0.
4. Solving these two equations, we have: x = 3/2 and x
= -4.
5. Checking our answers, we have:
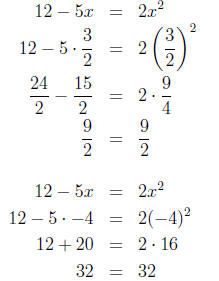
So, the solutions to the equation 12 - 5x = 2x2 are x = 3/2 and x
= -4.
•Quadratic Formula:
This method can be used for any quadratic equation. It
is not always the simplest method, but it will always work.
1. By adding and/or subtracting, move all the terms to one
side of the equa-
tion. There should just be a zero left on the other side of the equation.
2. The equation is in general form: ax2 + bx + c = 0. Identify a, b,
and c.
3. Plug a, b, and c into the quadratic formula:
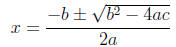
4. Simplify to find x.
5. Check the answers in the original equation.
Example 3 Solve x2 + 6 = 5x by using the
quadratic formula.
1. We want to move the 5x to the left-hand side, so we subtract 5x from both
sides, and we have:
x2 - 5x + 6 = 0
2. a = 1, b = -5, and c = 6.
3. Plugging into the formula, we have:
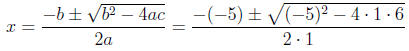
4. Simplifying this, we have:
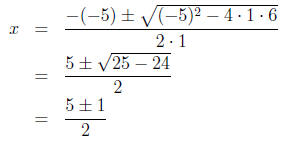
So, 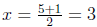 and and 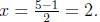
5. This is the same problem as Example 1, so, we have
already checked these
answers.
So, the solutions to the equation x2 + 6 = 5x are x = 3 and x = 2.
Example 4 Solve 2x = x2 + 2 by using
the quadratic formula.
1. We want to move the 2x to the right-hand side, so we subtract 2x from
both sides, and we have:
0 = x2 - 2x + 2
2. a = 1, b = -2, and c = 2.
3. Plugging into the formula, we have:
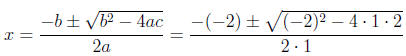
4. Simplifying this, we have:
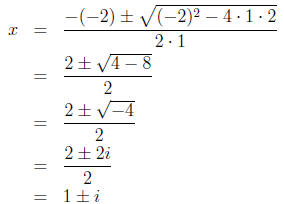
So, x = 1 + i and x = 1 - i.
5. Checking our answers, we have:
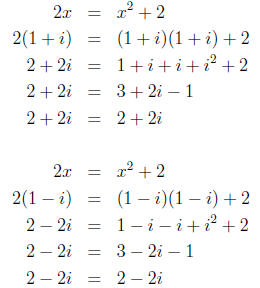
So, the solutions to the equation 2x = x2 + 2 are x = 1 + i and x
= 1 - i.
• Extracting Square
Roots: This method can only be used if there is only one
x in the equation.
1. By adding and/or subtracting terms, get the squared term by itself on one
side of the equation.
2. Take the square root of both sides. This will get rid of the square. You
must add a plus and minus (±) on the side of the equation
that doesn't
have the variable.
3. Get the variable by itself.
4. Check the answers in the original equation.
Example 5 Solve (2x + 1)2 - 9 = 0.
1. We want to move the ¡9 to the right-hand side, so we add nine to both
sides, and we have:
(2x + 1)2 = 9
2. Taking the square root of both sides, the equation
becomes: 2x + 1 =
±3.
3. Solve for x by subtracting one and dividing by two
on both sides, and we
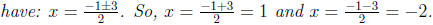
4. Checking the answers, we have:
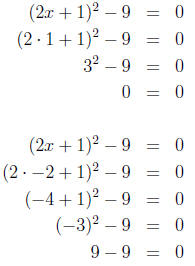
So, the solutions to the equation (2x + 1)2 - 9 = 0 are x = 1 and
x = -2.
• Practice Problems―
Solve the following equations using any method that
applies.
1. x2 - 2x - 8 = 0
2. x2 + 9 = 0
3. 2x2 - 5x + 2 = 0
4. y2 = 6y - 9
5. (3 ¡ x)2 - 7 = 0
6. 2t(4t + 1) = 3
7. 5x2 + 1 = 2x
• Answers:
1. x = 4 and x = -2
2. x = 3i and x = -3i
3. x = 2 and x = 1/2
4. y = 3
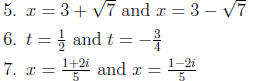
|