Solving Quadratic Equations by Factoring
1 Teaching objective(s)
A. Investigate and apply real number solutions to quadratic equations
algebraically and graphically.
B. Use technology to solve quadratic equations.
2 Instructional Activities
This lesson is to be taught as a review and reinforcement of algebraic methods
of
solving quadratic equations, therefore; class will begin with a review of some
of the
various methods that have been used to solve quadratic equations. The factoring
method
of solving quadratic equations will be briefly discussed with the following
example given
as a review:
Solving quadratic equations by factoring:
x² + 3x – 10 = 0
Since this equation is factorable it can be solved by
simply
factoring.
(x – 2)(x + 5) = 0
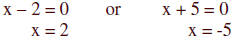
The quadratic formula method of solving quadratic equations will be reviewed as
a possible alternative method of solving non-factorable quadratic equations. The
following equation will be used as a review example:
x² + 7x = 10
Rearrange the equation equal so that it fits the form of
ax² + bx + c = 0.
x² + 7x – 10 = 0 Use the formula with the given
coefficients.
a= 1, b= 7, c = -10
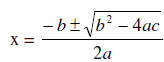
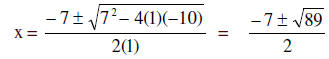
 the solution set is
the solution set is
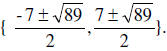
(20 minutes)
The remainder of the class period will be used to explore
the use of graphing
calculators to solve quadratic equations. Since most students are familiar with
using
calculators to graph equations, the graphing method will be explored first.
Students
must clearly understand that if a quadratic equation is viewed as a function,
then
finding the roots of the equation is the same as finding the zeros of the
function. A
few examples will be needed to illustrate the connection between the roots of
the
equation and the zeros of the function. The example problem from earlier will be
used to
show the method of finding the zeros (roots). The following instructions will be
given to
students on a handout:
Use the calculator to find quadratic roots:
x² + 3x – 10 = 0
Step 1. Press the Y= button.
Step 2. Type the equation (function) with y replacing the zero.
Step 3. Press the GRAPH button, then press the TRACE button.
Step 4. Find the point(s) where the function intersects the x-axis.
Step 5. Press 2nd and then GRAPH to get the table.
Step 6. Find the zero value(s) of the y-variable.
Step 7. Record the corresponding x-value(s) as your root(s).
( If the entire curve cannot be seen, it may be necessary to expand your domain
by
increasing your Xmin and Xmax by pressing WINDOW and increasing the
values).
The handout will also contain the following quadratic
formula program for the
calculator :
(This program was adapted to work on the TI-73 graphing
calculator, but a similar
program on the TI-81, TI-82 or higher model calculator can be found in:
Glencoe
Mathematics Graphing Calculators in the Mathematics Classroom. )
Step 1. To enter the program, press the PRGM button.
Step 2. Move the cursor over to NEW.
Step 3. Name the program QUADRATC.
Step 4. Press the PRGM button again to access all program commands.
Step 5. Type the following program:
|