Solving Quadratic Equations
8.1: The Square Root Property
Given an equation that looks like u2=d , be sure to isolate the u2 term, then
take the square
root of both sides. The answer will look like:
If d>0 , 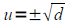 OR If d<0 , OR If d<0 ,
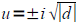
Because you are introducing the square root into the
problem, be sure to remember to add a the
 plus or minus sign!
plus or minus sign!
8.2: Completing the Square
Given a trinomial that does not factor, we can rewrite the equation by
constructing a perfect square
trinomial (completing the square).
First, move all constants to the right hand side, then complete the square by
adding (b/ 2)2 to
BOTH sides of the equation. The left hand side now factors as a perfect square
trinomial, and the
square root property from 8.1 can be used to finish the problem.
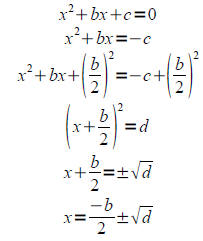
Remember! If the leading coefficient of your quadratic
equation is not one, you must divide all
terms by that coefficient to make the leading coefficient one BEFORE completing
the square.
8.3 The Quadratic Formula
Given ANY quadratic equation ax2+bx+c=0, a≠0 , you can use the quadratic
formula:
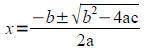
Keep in mind the following:
1. If b2−4ac>0 the equation has 2 real solutions
2. If b2−4ac=0 the equation has one repeated real solution
3. If b2−4ac<0 the equation has no real solutions (2 distinct complex solutions)
|