Solving Linear Equations - Part II

I. Solving Linear Equations
A. Get rid of all fractions by multiplying both sides by the LCD.
B. Simplify both sides.
C. Use the Addition Property to get all the variable terms on one side of the equal sign,
the constant terms on the other.
D. Use the Multiplication Property to isolate the variable.
E. Check your solution by substituting your answer back into the original equation.
F. Examples - Use properties of equality to isolate x on one side of the equation.



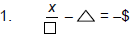
Let's multiply both sides by to clear the fraction.

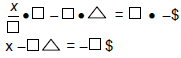	Simplify the LHS.
	Add 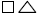to both sides to isolate the variable.

Answer: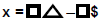

2. Now you try one: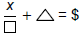

Answer: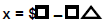

G. Applications

1. In Massachusetts, speeding fines are determined by the formula

F = 10(x – 65) + 50

where F is the cost, in dollars, of the fine if a person is caught driving x miles
per hour. Use this formula to solve exercise 74.

If the fine comes to $400, how fast was that person speeding? (Page 133,
#74)

Let F = The fine, in dollars
Let x = The speed, in mph

We are told to find the speed when the fine is $400, so we will substitute 400
in for F in the formula and solve for x.

400 = 10(x – 65) + 50	Distribute 10 on the right-hand side, but only to the terms in parentheses.
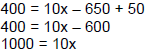	Simplify the right-hand side. Add 600 to both sides to isolate the x term. Divide by 10 to isolate x.
100 = x

Answer: The moron was going 100 mph!

2. The formula



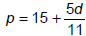
describes the pressure of sea water, p, in pounds per square inch (psi) at a
depth of d feet below the surface. Use the formula to solve exercises 78.

At what depth is the pressure 20 psi? (Page 133, #78)

Let p = The pressure, in psi
Let d = The depth, in feet

We want to find the depth at which pressure = 20 psi, so we need to
substitute 20 in for p and solve for d.

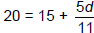	Clear the fraction by multiplying by the LCD, 11.
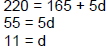	220 = 165 + 5d Subtract 165 from both sides to isolate the d term. 55 = 5d Divide both sides by 5 to isolate d.

Answer: At a depth of 11 feet, the pressure will be 20 psi.

3. Now you try one: The latest guidelines, which apply to both men and women, give
healthy weight ranges, rather than specific weights, for your height. The further you
are above the upper limit of your range, the greater are the risks of developing
weight-related health problems. The bar graph (bottom of left-hand column, page
133) shows these ranges for people between the ages of 19 and 34, inclusive.

The mathematical model



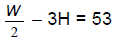
describes a weight, W, in pounds, that lies within the healthy weight range for a
person whose height is H inches over 5 feet. Use this information to solve exercise
75.

Use the formula to find the healthy weight for a person whose height is 5’ 6”. (Hint:
H = 6 because this person’s height is 6 inches over 5 feet.) How many pounds is
this healthy weight below the upper end of the range shown by the bar graph?

Answer:
Equation: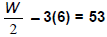
The healthy weight for someone 5’ 6” tall is 142 pounds. This is 13
pounds below the upper end of the range.