Solving a System of Linear Equations by Graphing

What is a system of Linear Equations?

A system of linear equations is a list of two linear equations that each represents the graph of a line.

Equation A		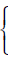y = −2x + 3
Equation B		y = 5x − 4

Equation A		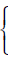y = 3x − 7
Equation B		y = 4

Equation A		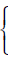2x + y =17
Equation B		x − y = 4

What is a solution to a system of Linear Equations?

The solution to a system of linear equations are any ordered pairs that make both equations true. If an
ordered pair (x, y) is solution to the system then when you put the values for the x and y coordinates
into BOTH equations then the ordered pair must make both equations true.

The examples below will list two equations labeled Equation A and Equation B and a point will be
given as a possible solution. The x and y coordinates of the point will be plugged into both equations
for the x and y variables. If that x and y pair makes both equations true then the point is a solution and
if does not it is not a solution.

Example 1

Is (7, 3) a solution to

Equation A		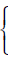2x + y =17
Equation B		x − y = 4

(7, 3) means x = 7 and y = 3

plug these values into both
Equation A and Equation B to
see if they work in both equations

x = 7 and y = 3

Equation A		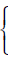2x + y =17	2(7) + (3) =17
Equation B		x − y = 4	7 −(3) = 4

(7, 3) works in both equations so
YES it is a solution.

Example 2

Is (−3, 4) a solution to

Equation A		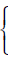−x + 2y = 9
Equation B		3x + y = −5

(−3, 4) means x = −3 and y = 4

plug these values into both
Equation A and Equation B to
see if they work in both equations

x = −2 and y = 4

Equation A		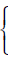−x + 2y = 9	−(−3) + 2(4) =11
Equation B		3x + y = −5	3(−3) + (4) = −5

(−3, 4) does not work in Equation A so
NO it is not a solution.

Example 3

Is (−6,4) a solution to

Equation A		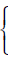3x + 2y =10
Equation B

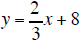(−6,4) means x = −6 and y = 4

plug these values into both
Equation A and Equation B to
see if they work in both equations

x = −6 and y = 4

Equation A		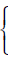3x + 2y =10	3(−6) + 2(4) = −10
Equation B

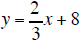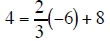(−6,4) Does NOT work in Equation A
so NO it is not a solution.

Example 4

Is(1/2,2/3)a solution to

Equation A		2x −6y = −3
Equation B		4 x + 3y = 4

(1/2,2/3) means x = 1/2 and y = 2/3

plug these values into both
Equation A and Equation B to
see if they work in both equations

x = 1/2 and y = 2/3

Equation A		2x −6y = −3
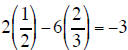Equation B		4 x + 3y = 4

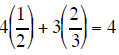(1/2,2/3) works in both equations
so YES it is a solution.

Solving a System of Linear Equations by Graphing

In this chapter we will list two linear equations and ask you to graph each of them on the same graph.
Each line will go through points that make it’s equation true. We will be trying to find a point that makes
both equations true at the same time. The solution to the system is an ordered pair that
makes both equations true.

Example 1

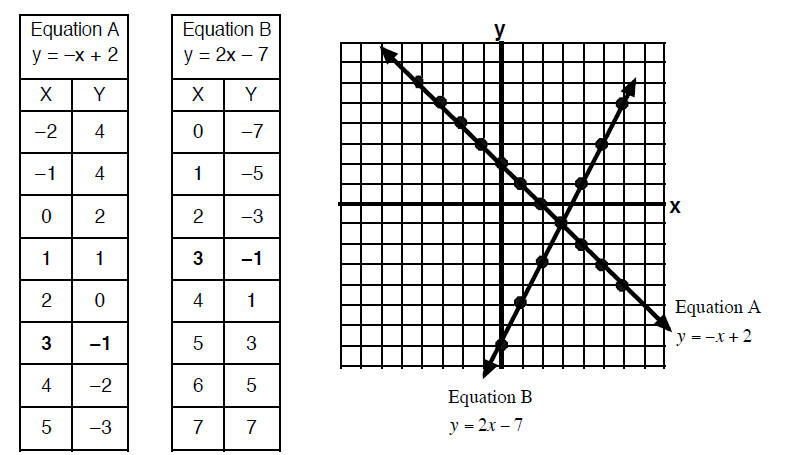
Equation A		y = −x + 2
Equation B		y = 2x − 7

Any point on the line that represents Equation A is a solution to Equation A. Several points have
been highlighted on the graph that are solutions to Equation A. The table for those points shows
several of the infinite number of ordered pairs that make that equation true. The same has been done
for the line that represents Equation B. As you can see, the points on Equation A are different then the
points for Equation B except in one case. The point (3, –1) is the only point that is is on both lines. It
is the only ordered pair that will make both equations true. We call the point (4, –1) the solution to the
system of two lines.

The point (3, –1) is the solution to the system of two lines.

Check to see if (3,–1) is a solution

Equation A		y = −x + 2	−1= −(3) + 2	is true
Equation B		y = 2x − 7	−1 = 2(3) − 7	is true

Example 2

Solve the system of equations by graphing.
List your answers as an ordered pair.

Equation A
Equation B

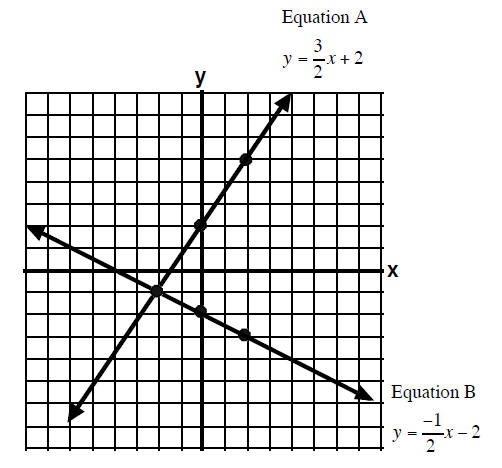
The lines have intersect at the point (–2, –1). That point is on both lines and
the x and y values will make both Equation A and Equation B true.

Answer: (−2,−1)

Check:

Equation A		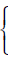		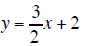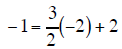True
Equation B		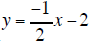		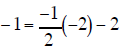True

Example 3

Solve the system of equations by graphing.
List your answers as an ordered pair.

Equation A
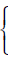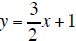Equation B		−x + 2y =10

First Solve Equation B for y

Equation A
Equation B

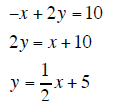
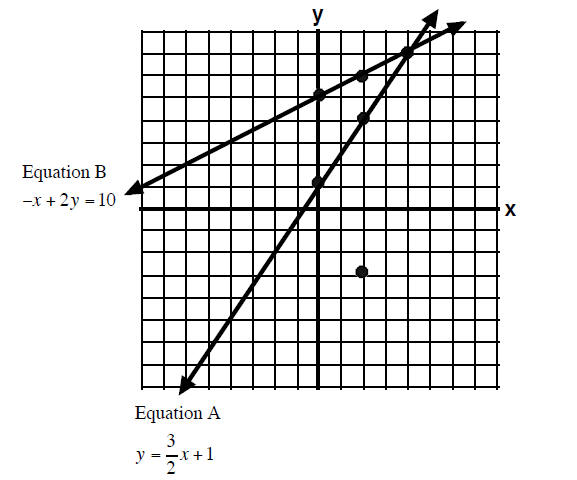
The lines intersect at the point (4, 7). That point is on both lines and
the x and y values will make both Equation A and Equation B true.

Answer: (4,7)

Check:

Equation A		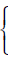		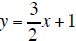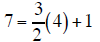True
Equation B		−x + 2y =10	−(4) + 2(7) =10	True

Do all systems intersect at a point and have one ordered pair as a solution?

The graphs of the system of two lines can have three possible outcomes. Each of the different
possible outcomes has a different format for the answer.

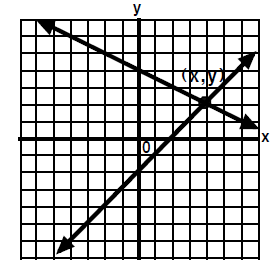1. The lines have one point in common. The lines intersect at one point. If two lines cross over each other then they will have exactly one point in common. The x and y coordinates of that point will make both equations true. That point is the solution to the system. Answer: (x , y)

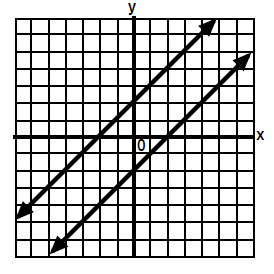2. The lines have no points in common. The lines are parallel If two lines have the same slope and different y intercepts then they are parallel and they will have no points in common. There are no x and y coordinates that point will make both equations true. Answer: No Solution

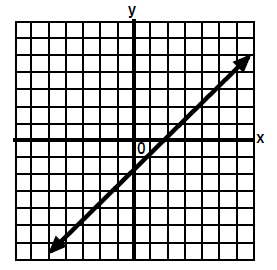3. The lines coincide. When you graph both lines they lie on top of one another. The two lines have the same equation and all the points on one line are also on the other line. All the points on the linear equation will make both equations true. Answer: All points on y = mx + b where the actual equation is written in place of the y = mx + b

Examples of the three possible outcomes.

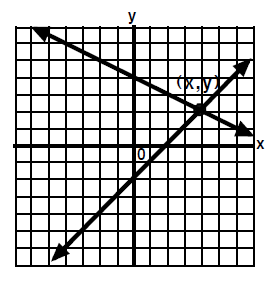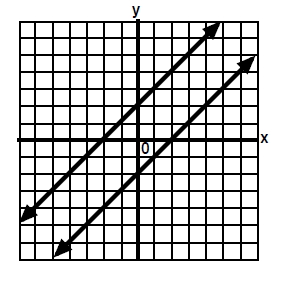
1. The lines have one point in common. Equation A 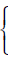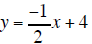Equation B y = x − 2 the lines cross at the point (4,2) Answer: (4 , 2)

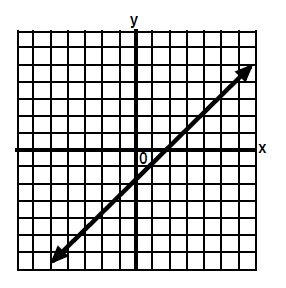
2. The lines have no points in common. Equation A 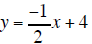Equation B y = x − 2 The lines are parallel and do not have any points in common. Answer: No Solution

3. The lines coincide. Equation A 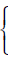−x + y = −2 Equation B y = x − 2 when you solve Equation A for y you get Equation A 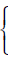y = x − 2 Equation B y = x − 2 Equations A and B are the same line so all the points that make Equation A true make Equation B true also. Answer: All points on y = x −2