Systems of Linear Equations in Three Variables and Matrix
Operations
Systems in Three Variables
Systems of the form
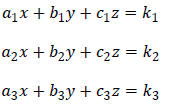
are called linear equations in three variables. A triplet of numbers
(x,y,z) is a solution of the system if EACH equation is satisfied by the
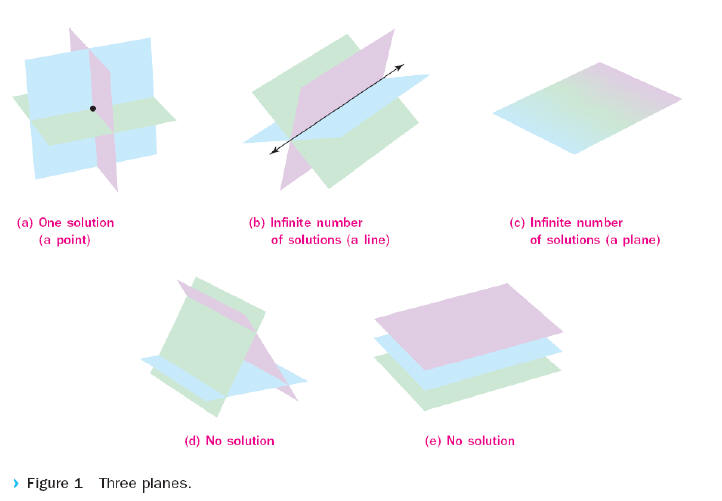
triplet. Figure 1 (p. 483) shows several of the many ways in which three planes
can intersect:
Using Elimination by Addition
The general approach to solving a system with three variables is to use Theorem
2 in the last section to eliminate variables until an equivalent system with an
obvious solution is obtained. We will refer to the equations in a system as E1,
E2, and so on.
Example 1: Solve:
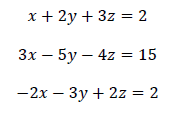
Performing Row Operations on Matrices
A matrix is a rectangular array of numbers written within
brackets. Each number in a matrix is called an element of the matrix. If a
matrix has m rows and n columns, it is called an m×n matrix. The
expression m×n is called the size of the matrix, and the numbers m and n are
called the dimensions of the matrix.
*Note:
If the number of rows is equal to the number of columns,
then the matrix is called a square matrix. A matrix with only one column is
called a column matrix, and a matrix with only one row is called a row matrix.
Ex.
The position of an element in a matrix is the row and
column containing the element. This is usually denoted using double subscript
notation aij,
where i is the row and j is the column containing the element
aij.
Ex.
The principal diagonal of a matrix consists of the
elements aii, i=1,2,…,n.
Example 1: Write the augmented coefficient matrix corresponding to each of the
following systems.
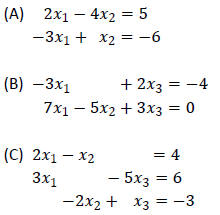
Recognizing Reduced Matrices
Example 3: Write the system corresponding to each of the following augmented
coefficient matrices and find its solution.
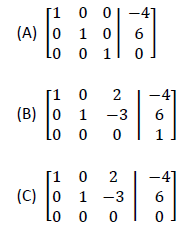
*Note:
Go back and try example 1 using matrices.
Recognizing Inconsistent and Dependent Systems
As with systems with two variables and two equations, if
you obtain an inconsistent equation (such as 0=1) while solving a system, then
the system is inconsistent and has no solution. On the other hand, if you obtain
an equation that is always true (such as 0=0), then the system may be
inconsistent (no solution) OR dependent (infinite number of solutions). The
solution process must proceed further to determine which is the case.
Example2: Solve:
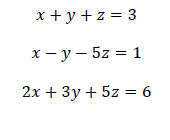
Example 3: Solve:
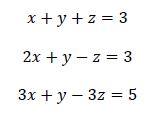
Modeling with Systems in Three Variables
Example 4: A garment industry manufactures three shirt styles. Each style shirt
requires the services of three departments as listed in the table. The cutting,
sewing, and packaging departments have available a maximum of 1,160, 1,560, and
480 labor-hours per week, respectively. How many of each style shirt must be
produced each week for the plant to operate at full capacity?
| |
Style A |
Style B |
Style C |
Time available |
| Cutting department |
0.2 hr |
0.4 hr |
0.3 hr |
1,160 hr |
| Sewing department |
0.3 hr |
0.5 hr |
0.4 hr |
1,560 hr |
| Packaging department |
0.1 hr |
0.2 hr |
0.1 hr |
480 hr |
Example 5: In 2001 there were 110 million cell phone
subscribers in the United States. This number grew to 128 million in 2002 and
141 million in 2003. Construct a model for these data by finding a quadratic
function whose graph passes through the points (1,110), (2,128), and (3,141).
Use this model to estimate the number of subscribers in 2004 and 2005.
|