Solving Quadratic Equations

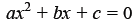
Four Methods:

1. Factoring (and ZPP),
2. Square Root Method,
3. Completing the Square, and
4. Quadratic Formula

Some methods work better for certain kinds of problems.

Method 1: Factoring and the ZPP

Method 2: Square Root Method

The SRP (square root principle) states:

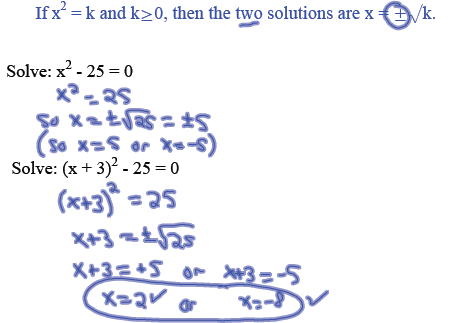
Method 3: Complete the Square

A perfect square trinomial (PST) has the form
(x+d)^2 = x^2 + 2dx + d^2.

Solve by completing the square and applying the square root
principle:

Method 4: The Quadratic Formula:

Before we practice, let's review what we have so far:
Method 1: Factor and use ZPP
Method 2: Use the Square Root Principle, if applicable.
Method 3: Complete the Square, then use Method 2.
Method 4: Use the Quadratic Formula, then Simplify.

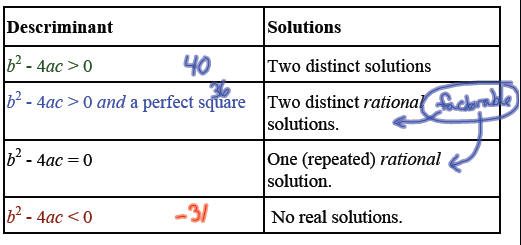
The expression b^2-4ac is called the discriminant.

We can use the discriminant to determine the types of solutions we
can expect.

Complete the table below:

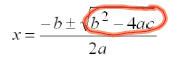
No real solutions.
One (repeated) rational solution.
Two distinct rational solutions.
Two distinct solutions

Developing Understanding:

1. How can we use the quadratic formula to determine whether a
quadratic equation is factorable?

e.g. Is 4x + 3x^2 + 7 factorable?

2. Given the quadratic equation -2x^2+ bx + 8. Is it possible to
find b so that the quadratic equation has:
a) two rational solutions,
b) two real (non-rational) solutions,
c) one real solution,
d) no real solutions?

For each of the above, find b (if possible) OR explain why it is
not possible.