SOLVING QUADRATIC EQUATIONS USING THE QUADRATIC FORMULA
10.1A SOLVING QUADRATIC EQUATIONS USING THE QUADRATIC
FORMULA
Review of Square Roots:
Recall, the square root of a number is a number that when multiplied by
itself, gives the
original number.
For example: 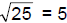 because 52 = 25 because 52 = 25
25 is a perfect square because it has a rational square root. You
may use your calculator to
evaluate the square root of values that are not perfect squares.
For example, 13 is not a perfect square because it has an irrational
square root, which means
that its square root is a decimal number which never ends or repeats. However,
by using a
calculator, we can find that 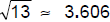 if we round to
three decimal places. if we round to
three decimal places.
Quadratic Formula:
In addition to solving by factoring, quadratic equations may be solved by using
the Quadratic
Formula:
For any quadratic equation written in standard form: ax2 + bx + c = 0
with a ≠ 0,
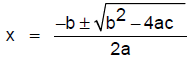
The Quadratic Formula may be used to solve quadratic
equations which may be factored as
well as those which cannot be factored or are difficult to factor.
Example 1: Solve using the quadratic formula: 4x2 + 5x = 6
First write the equation in standard form: 4x2 + 5x – 6 = 0
Then a = 4, b = 5, and c = –6. Substitute these values into the quadratic
formula:
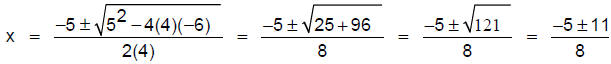
This gives two answers:
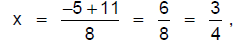 or or
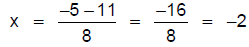
Note that the equation could have been solved by
factoring: (4x – 3)(x + 2) = 0
Set each factor equal to zero: 4x – 3 = 0 or x + 2 = 0
Solving each of these equations gives the same solutions
as the quadratic formula
gave: 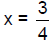 or x = –2. or x = –2.
Example 2: Solve using the quadratic formula: m2 – m – 2 = 4m – 5
First write the equation in standard form by subtracting 4m from both sides and
adding
5 to both sides of the equation: m2 – 5m + 3 = 0
Then a = 1, b = –5, and c = 3. Substitute these values into the quadratic
formula:
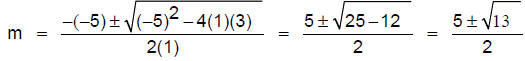
This gives two answers:
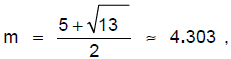 or or
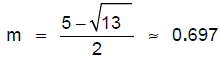
Note that 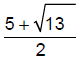 and and 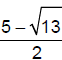 are
exact answers, while 4.303 and 0.697 are are
exact answers, while 4.303 and 0.697 are
approximations to three decimal places.
10.1B MORE APPLICATIONS OF QUADRATIC EQUATIONS
The following examples are applications of quadratic equations.
Example 3: Five times a number is 24 less than the square of that number. Find
all such
numbers.
Let n = the number.
Then 5n = n2 – 24.
Write this equation in standard form by subtracting 5n from both sides:
0 = n2 – 5n – 24, or n2 – 5n – 24 = 0.
You may solve this equation either by factoring or by using the quadratic
formula.
Factoring gives (n + 3)(n – 8) = 0.
Set each factor equal to zero: n + 3 = 0, or n – 8 = 0.
Then solve each of these equations to get n = –3 or n = 8.
The number is –3 or 8 (you must give both answers).
Check the answers in the original problem:
5(–3) = (–3)2 – 24 which gives –15 = –15 , and
, and
5(8) = (8)2 – 24 which gives 40 = 40
 . .
Example 4: The product of two consecutive odd integers is 195. Find the
integers.
Let x = the first odd integer.
Then x + 2 = the next odd integer (because odd numbers are two apart).
The equation is x (x + 2) = 195.
Distribute the x, and then subtract 195 from both sides of the equation to write
the
equation in standard form: x2 + 2x – 195 = 0.
Again, you may solve this equation either by factoring or by using the quadratic
formula.
Factoring gives (x + 15)(x – 13) = 0.
Set each factor equal to zero: x + 15 = 0, or x – 13 = 0.
Then solve each of these equations to get x = –15 or x = 13.
For each of these answers, find the next odd integer by adding two to your
answer:
For the first answer, –15, the next odd integer is x + 2 = –15 + 2 = –13.
For the second answer, 13, the next odd integer is x + 2 = 13 + 2 = 15.
The odd integers are –15 and –13, or the odd integers are 13 and 15 (you must
give
both pairs of answers).
Check the answers by multiplying:
(–15)(–13) = 195 , and , and
(13)(15) = 195 . .
Example 5: The length of one leg of a right triangle is 9 meters. The length of
the hypotenuse
is three meters longer than the other leg. Find the length of the hypotenuse and
the
length of the other leg.
Let x = the length of the other leg in meters.
Then x + 3 = the length of the hypotenuse in meters.
Use the Pythagorean Theorem, a2 + b2 = c2, to
solve the problem:
x2 + 92 = (x + 3)2.
When simplified, the equation becomes x2 + 81 = x2 + 6x +
9 (don't forget that the
square of a binomial is a trinomial).
When x2 is subtracted from both sides of the equation, the equation
becomes:
81 = 6x + 9, which is no longer a quadratic equation
because it has no x2 term.
Solve as a linear equation by subtracting 9 from both sides and then dividing by
6:
72 = 6x, or 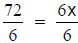 , which becomes 12 = x. , which becomes 12 = x.
Therefore, the length of the other leg is x = 12 meters.
The length of the hypotenuse is x + 3 = 12 + 3 = 15 meters.
Check by using the Pythagorean Theorem:
122 + 92 = 152, or
144 + 81 = 225, or
225 = 225  . .
In addition to the problems assigned from your Personal
Academic Notebook for lesson 10.1,
work the following problems.
Solve the quadratic equations below either by factoring or by using the
quadratic formula.
Give exact answers, and where appropriate, give approximations to three decimal
places.
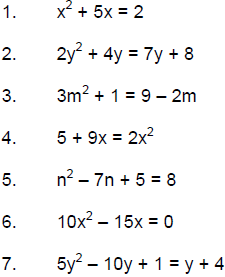
8. Four times a number is 12 less than the square of that
number. Find all such numbers.
9. The product of two consecutive odd integers is 143. Find the two integers.
10. The sum of the squares of two consecutive integers is nine less than ten
times the
larger. Find the two integers.
11. The length of a rectangular garden is 3 feet longer than the width. If the
area of the
garden is 88 square feet, find the dimensions of the garden.
12. A triangle has a base that is 2 cm longer than its height. The area of the
triangle is 12
square cm. Find the lengths of the height and the base of the triangle.
13. For an experiment, a ball is projected with an initial velocity of 48
feet/sec. Neglecting
air resistance, its height H, in feet, after t seconds is given by the formula
H = 48t – 16t2
How long will it take for the ball to hit the ground? (Hint: H = 0 when it hits
the ground.)
14. The length of one leg of a right triangle is 8 inches. The length of the
hypotenuse is four
inches longer than the other leg. Find the length of the hypotenuse and the
length of
the other leg.
15. A water pipe runs diagonally under a rectangular garden that is one meter
longer than it
is wide. If the pipe is 5 meters long, find the dimensions of the garden.
ANSWERS:
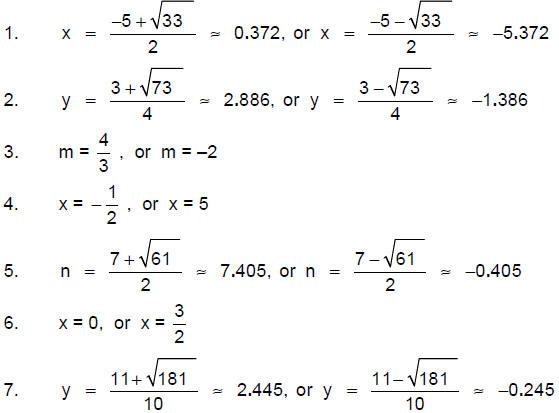
8. The number is –2 or 6. [Equation is 4x = x2
– 12]
9. The odd integers are 11 and 13, or the odd integers are –13 and –11.
[Equation is x (x + 2) = 143]
10. The consecutive integers are 0 and 1, or the consecutive integers are 4 and
5.
[Equation is x2 + (x + 1)2 = 10(x + 1) – 9]
11. The width is 8 feet, and the length is 11 feet. Note that dimensions of
geometric
figures cannot be negative. [Equation is x (x + 3) = 88]
12. The height is 4 cm, and the base is 6 cm. [Equation is
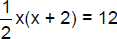 ] ]
13. The ball will hit the ground in 3 seconds. [Equation is 0 = 48t – 16t2]
14. The other leg is 6 inches, and the hypotenuse is 10 inches.
[Equation is x2 + 82 = (x + 4)2]
15. The width is 3 meters, and the length is 4 meters.
[Equation is x2 + (x + 1)2 = 52]
|