Free Algebra
Tutorials!


	Home
	Systems of Linear Equations and Problem Solving
	Solving Quadratic Equations
	Solve Absolute Value Inequalities
	Solving Quadratic Equations
	Solving Quadratic Inequalities
	Solving Systems of Equations Row Reduction
	Solving Systems of Linear Equations by Graphing
	Solving Quadratic Equations
	Solving Systems of Linear Equations
	Solving Linear Equations - Part II
	Solving Equations I
	Summative Assessment of Problem-solving and Skills Outcomes
	Math-Problem Solving:Long Division Face
	Solving Linear Equations
	Systems of Linear Equations in Two Variables
	Solving a System of Linear Equations by Graphing
	Ti-89 Solving Simultaneous Equations
	Systems of Linear Equations in Three Variables and Matrix Operations
	Solving Rational Equations
	Solving Quadratic Equations by Factoring
	Solving Quadratic Equations
	Solving Systems of Linear Equations
	Systems of Equations in Two Variables
	Solving Quadratic Equations
	Solving Exponential and Logarithmic Equations
	Solving Systems of Linear Equations
	Solving Quadratic Equations
	Math Logic & Problem Solving Honors
	Solving Quadratic Equations by Factoring
	Solving Literal Equations and Formulas
	Solving Quadratic Equations by Completing the Square
	Solving Exponential and Logarithmic Equations
	Solving Equations with Fractions
	Solving Equations
	Solving Linear Equations
	Solving Linear Equations in One Variable
	Solving Linear Equations
	SOLVING QUADRATIC EQUATIONS USING THE QUADRATIC FORMULA
	SOLVING LINEAR EQUATIONS

Try the Free Math Solver or Scroll down to Tutorials!

Enter expression, e.g. (x^2-y^2)/(x-y)

Enter expression, e.g. x^2+5x+6

Enter expression, e.g. (x+1)^3

Enter a set of expressions, e.g. ab^2,a^2b

Enter equation to solve, e.g. 2x+3=4

Enter equation to graph, e.g. y=3x^2-1

Depdendent Variable

Number of equations to solve:

Equ. #1:

Equ. #2:

Equ. #3:

Equ. #4:

Equ. #5:

Equ. #6:

Equ. #7:

Equ. #8:

Equ. #9:

Solve for:

Enter inequality to solve, e.g. 2x+3>4

Enter inequality to graph, e.g. y<3x^2-1

Dependent Variable

Number of inequalities to solve:

Ineq. #1:

Ineq. #2:

Ineq. #3:

Ineq. #4:

Ineq. #5:

Ineq. #6:

Ineq. #7:

Ineq. #8:

Ineq. #9:

Solve for:

Math solver on your site

Please use this form if you would like
to have this math solver on your website,
free of charge.

Name:

Email:

Your Website:

Msg:

Solving Rational Equations

Rational equations are simply equations with rational expressions in them. We can use the technique outlined earlier to clear the fractions of a rational equation. After clearing the fractions we will be left with either a linear or quadratic equation that can be solved as usual.



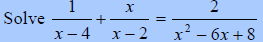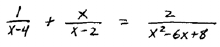Step 1: Factor the denominators.		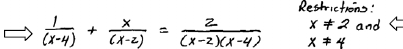Step 2: Identify the restrictions.
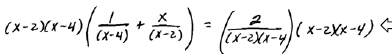		Step 3: Multiply both sides by the LCD.
Step 4: Solve like normal. In this case solve the resulting quadratic equation.
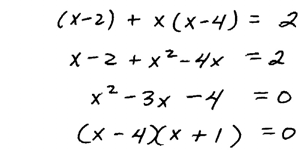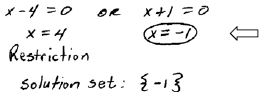		Step 5: Check answers against the restrictions.

This process sometimes produces answers that do not solve the original equation, so it is extremely important to check them. Tip: It suffices to check that the answers are not restrictions to the domain of the original equation.

A. Solve

Determining the LCD is the step that most students have difficulty with. When deciding what the LCD is, use one of each factor, make sure that when we multiply it cancels with all the denominators and clears the fractions. If it does not, the LCD is incorrect.

B. Solve

If we multiply both sides by the LCD we would next distribute it through the expression. We can save this step and simply multiply every term of the rational expression by the LCD as illustrated below.

It is tempting to simply multiply all the factors of the denominator together to obtain a common multiple. This will work, but usually leaves us with an equation that is too cumbersome to work with. If we use the Least Common multiple of all the factors in the denominators then we will have less factoring in the end. Bottom line, it is worth spending the extra time to find the LCD.

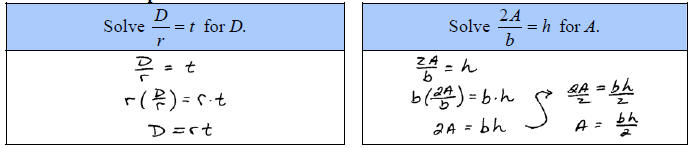
Some literal equations, often referred to as formulas, are also rational equations. Use the techniques of this section and clear the fractions before solving for the particular variable.

C. Solve for the specified variable

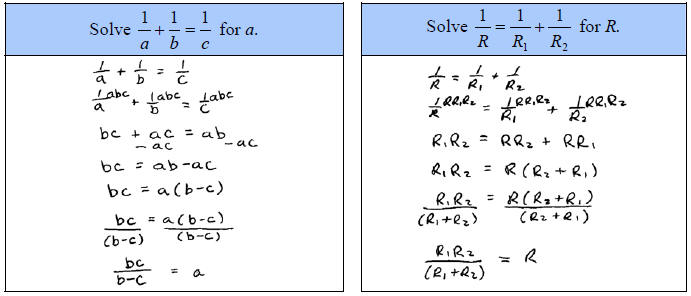
The reciprocal of a number is the number we obtain by dividing 1 by that number. Often we think of the reciprocal as an interchange of the numerator and denominator but this definition fails us when the number to be reciprocated is a variable.

C. Typical Number Problem