Systems of Linear Equations in Two Variables

Questions

1. Solve the system by graphing:

3x + y = 2
2x − y = 3

2. Solve the system by graphing:

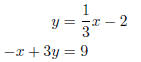
3. Solve the system by graphing:
y = −2x + 5
3y + 6x = 15

4. Solve the system algebraically, using any method you like:
4x + 3y = 9
3y + 6 = x

5. Solve the system algebraically, using any method you like:
5x + 2y = 5
3x + y = 4

6. Solve the system algebraically, using any method you like:
4x + 2y = 4
3x + y = 4

7. Solve the system algebraically, using any method you like:
9x + 2y = 2
3x + 5y = 5

8. Solve the system algebraically, using any method you like:
6s − 3t = 1
5s + 6t = 15

9. Solve the system algebraically, using any method you like:
0.2x = 0.1y − 1.2
2x − y = 6

Solutions

To solve by sketching, we should use graph paper, or be very careful with the scale as we sketch by hand. Whenever
you are reading a solution off of a graph you need to be very precise! That’s why we prefer algebra to solve systems of
equations.

1. You can sketch this using techniques from previous sections (slope and y-intercept, or getting two points).
Sketch 3x + y = 2:

When x = 0 -> 3(0) + y = 2 -> y = 2, so the ordered pair is (0, 2).
When y = 0 -> 3x + (0) = 2 -> x = 2/3, so the ordered pair is (2/3, 0).

Sketch 2x − y = 3:
When x = 0 -> 2(0) − y = 3 -> y = −3, so the ordered pair is (0,−3).
When y = 0 -> 2x − (0) = 3 -> x = 3/2, so the ordered pair is (3/2, 0).

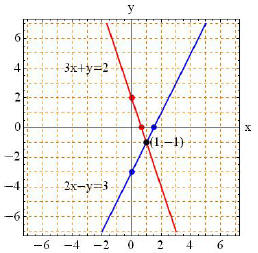
The solution to the system appears to be (1,−1). Check by substituting into the original equations:
3(1) + (−1) = 2 True
2(1) − (−1) = 3 True

2. You can sketch this using techniques from previous sections (slope and y-intercept, or getting two points).
Sketch y = 1/3x − 2:

When x = 0 -> y =1/3(0) − 2 -> y = −2, so the ordered pair is (0,−2).
When y = 0 -> 0 =1/3x − 2 -> x = 6, so the ordered pair is (6, 0).

Sketch −x + 3y = 9:
When x = 0 -> −(0) + 3y = 9 -> y = 3, so the ordered pair is (0, 3).
When y = 0 -> −x + 3(0) = 9 -> x = −9, so the ordered pair is (−9, 0).

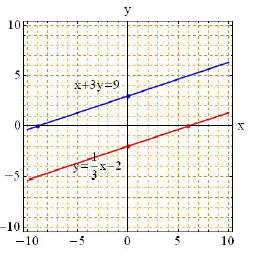
The system has no solution, since the lines are parallel. Check by computing the slope of each line (parallel lines have the same slope).

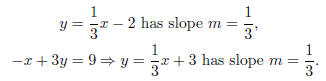
3. You can sketch this using techniques from previous sections (slope and y-intercept, or getting two points).
Sketch y = −2x + 5:

When x = 0 -> y = −2(0) + 5 -> y = 5, so the ordered pair is (0, 5).
When y = 0 -> 0 = −2x + 5 -> x = 5/2, so the ordered pair is (5/2, 0).

Sketch 3y + 6x = 15:
When x = 0 -> 3y + 6(0) = 15 -> y = 5, so the ordered pair is (0, 5).
When y = 0 -> 3(0) + 6x = 15 -> x = 5/2, so the ordered pair is (5/2, 0).

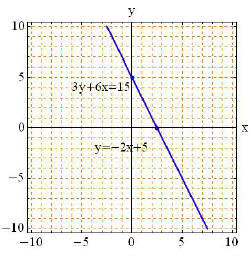
The system has an infinite number of solutions, since the lines are identical. Check by showing the lines have the same
equation. We can see that second equation is just the first equation multiplied by 3.
y = −2x + 5
3y + 6x = 15

4. Let’s use the substitution method.
From the second equation, we can solve for x = 3y + 6. Substitute this into the first equation:

4x + 3y = 9
4(3y + 6) + 3y = 9 now, solve for y
12y + 24 + 3y = 9
15y = 9 − 24
15y = −15
y = −1

Now, use this value of y in x = 3y + 6 to determine x:
x = 3y + 6
x = 3(−1) + 6
x = 3

The solution to the system is the ordered pair (3,−1). You can check by substituting this back into both original equations.
They should both be true when x = 3 and y = −1.

5. Let’s use the substitution method.
From the second equation, we can solve for y = 4 − 3x. Substitute this into the first equation:

5x + 2y = 5
5x + 2(4 − 3x) = 5 now, solve for x
5x + 8 − 6x = 5
−x = 5 − 8
−x = −3
x = 3

Now, use this value of x in y = 4 − 3x to determine y:
y = 4 − 3x
y = 4 − 3(3)
y = −5

The solution to the system is the ordered pair (3,−5).

6. Let’s use the substitution method.
From the second equation, we can solve for y = 4 − 3x. Substitute this into the first equation:

4x + 2y = 4
4x + 2(4 − 3x) = 4 now, solve for x
4x + 8 − 6x = 4
−2x = 4 − 8
−2x = −4
x = 2

Now, use this value of x in y = 4 − 3x to determine y:
y = 4 − 3x
y = 4 − 3(2)
y = −2

The solution to the system is the ordered pair (2,−2).

7. Let’s use the elimination method.
Multiply the second equation by −3 to make the coefficient of x the same in both equations, but with opposite sign.

9x + 2y = 2
−9x − 15y = −15

Now add the two equations to eliminate the x (since 9x − 9x = 0):
9x + 2y = 2
−9x − 15y = −15

Adding:
2y − 15y = 2 − 15 now solve for y
−13y = −13
y = 1

Now, use this value of y in any of the earlier equations to determine x:
9x + 2y = 2
9x + 2(1) = 2
9x + 2 = 2
9x = 0
x = 0

The solution to the system is the ordered pair (0, 1).

8. Let’s use the elimination method.
Multiply the first equation by 2 to make the coefficient of t the same in both equations, but with opposite sign.
12s − 6t = 2
5s + 6t = 15

Now add the two equations to eliminate the t (since −6t + 6t = 0):
12s − 6t = 2
5s + 6t = 15

Adding:
17s = 17 now solve for s
s = 1

Now, use this value of s in any of the earlier equations to determine t:

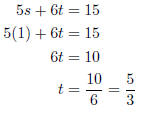
The solution to the system is the ordered pair

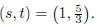
8. Let’s use the elimination method.
Multiply the first equation by −10 to make the coefficient of x the same in both equations, but with opposite sign.
−2x = −y + 12
2x − y = 6

Now add the two equations to eliminate the x (since −2x + 2x = 0):
−y = −y + 12 + 6
0 = 18

You might think you’ve made a mistake, but you just need to interpret what you’ve found.
Since 0 can never equal 18, there is no solution to the system of equations. Graphically, the two equations represent two
parallel lines.