Solving Quadratic Equations
An equation that can be simplified to the form
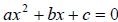 is called a quadratic equation. If the
equation is already simplified to this form we say it is in standard form. We
have already investigated two techniques for solving quadratic equations:
extraction of roots (which works if there is no linear term) and factoring.
Neither technique is practical in all cases. We will now investigate a technique
that is practical more generally.
Using the Quadratic Formula
The quadratic formula lets us find the solutions of a quadratic equation
when it is written in standard
form. 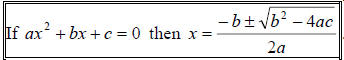 The plus or minus symbol (±) allows us
to represent both solutions in a single expression. Lets take a look at an
example to see how it works.
Example: Use the quadratic formula to find the solutions
to the equation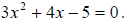 
Solution: First we identify the coefficients a, b and c
for this equation: a = 3, b = 4 and c = −5. Then we substitute these values for
a, b and c in the formula:
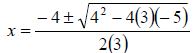
Let’s represent each solution separately and use our
calculators to approximate the solutions.
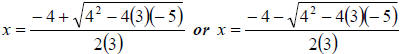
We can enter each of these solutions into our graphing
calculators with a single entry but we must pay careful attention to the order
of operations. Let’s start with the first solution. Enter it into your
calculator as follows:
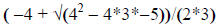
When you push enter the calculator should return the value
.7862996478
This is an approximation of the first solution. Now we
turn our attention to the second solution. Press 2nd Enter to bring up the
previous entry:
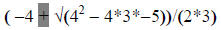
The entry for the second solution is identical except that
the addition that I’ve highlighted above should be changed to a subtraction:
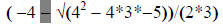
When you push enter the calculator should return the value
−2.119632981
So the solutions to the equation are approximately x =
.7862996478 and x = −2.119632981
|
