Solving Systems of Linear Equations

There are two basic methods we will use to solve systems of linear
equations:
• Substitution
• Elimination

We will describe each for a system of two equations in two unknowns,
but each works for systems with more equations and more unknowns.
So assume we have a system of the form:

ax + by = c
dx + ey = f

Substitution

To use substitution, we solve for one of the variables in one of the
equations in terms of the other variable and substitute that value in
the other equation.

That gives us a single equation in one variable, which we may solve
and then substitute that solution into either original equation or, even
better, into the formula we got for the other variable.

Elimination

With elimination, we legally modify the equations so that, for one
variable, its coefficients in the two equations match up, being either
the same or negatives of one another.

When the coefficients match up, we either add or subtract, meaning
we equate either the sum or difference of the left sides of the two equations
together with the sum or difference of the right sides of the two
equations.

Elimination

For example, given the equations

(1) ax + by = c
(2) dx + ey = f,

we might multiply both sides of (1) by d to get

(3) adx + bdy = cd
and multiply both sides of (2) by a to get

(4) adx + aey = af.
Elimination
Since the coefficients of x are the same, we equate the differences of
the two sides, getting

(5) (bd − ae)y = cd − af.
We can then solve (5) by dividing both sides by bd − ae to get y =

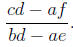
We can then either plug this value into any of the equations, or perform
a similar calculation to eliminate y and solve for x.

Example

Solve

2x + 5y = 16
3x + 2y = 13

We might multiply both sides of the first equation by 3 and the second
by 2, getting

6x + 15y = 48
6x + 4y = 26.

Subtracting, we get 11y = 22, y = 2.
We can substitute that into the first equation to get 2x + 5 · 2 = 16,
2x + 10 = 16, 2x = 6, x = 3.

Steps We May Take to Solve Equations

Every step taken to solve an equation or a system of equations may
be categorized as one of the following.

• Adding the same thing to both sides of an equation.
• Subtracting the same thing from both sides of an equation.
• Multiplying both sides of an equation by the same non-zero
thing.
• Dividing both sides of an equation by the same non-zero thing.
• Replacing something by something else equal to it.
• Raising both sides of an equation to the same power. Beware
that this step may introduce extraneous solutions.

Elementary Operations on Systems of Linear Equations

We will come up with a mechanical method for solving systems of
linear equations called Gaussian Elimination. It will not always be
the most efficient way when solving equations by hand, but will be an
excellent way to instruct a computer to use and will also lead to greater
understanding of the Simplex Method for solving linear programming
problems.

We will first reduce the steps we take to solve equations to just three
and see how these suffice for solving systems of linear equations. We
will use slang to denote these steps; it’s important to recognize what
we really mean.

The Three Elementary Row Operations

(1) Multiply an equation by a non-zero constant. Obviously, this
is something that should not be taken literally. What’s really
meant is to multiply both sides of an equation by the same nonzero
constant to obtain a new equation equivalent to the original
equation.

(2) Add a multiple of one equation to another. Again, this should
not be taken literally. It really means to add a multiple of the
left side of one equation to the left side of another and also add
the same multiple of the right side of that equation to the right
side of the other.

(3) Interchange two equations. This is obviously legitimate but may
seem pointless. It is essentially pointless if solving equations by
hand but will not be pointless when instructing a computer to
solve a system of equations.

Elementary Row Operations on Matrices

When solving equations using elimination, the variables themselves
are almost superfluous. One could change the names of the variables
and perform exactly the same steps, or even just write down the coefficients,
do arithmetic using the coefficients, and interpret the results.

When we write down the coefficients in an organized, rectangular array,
we get something called a matrix. A matrix is simply a rectangular
array of numbers.

Consider the following example, where we solve a system of two equations
in two unknowns, simultaneously performing analogous operations
on the coefficients.

Example

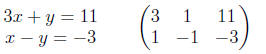
We’ll now add the second equation to the first to eliminate y from
the first equation. Simultaneously, we’ll add each of the coefficients in
the second row to the coefficients in the first row.

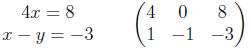
Now we’ll divide both sides of the first equation by 4 and simultaneously
divide the coefficients in the first row of the matrix to the right by 4.

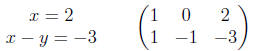
Example

Now we can eliminate x fromn the second equation by subtracting the
first from the second. Simultaneously, we will subtract the coefficients
in the first row of the matrix from the coefficients in the second row.

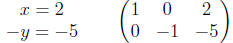
Finally, we’ll multiply the second equation by −1 and simultaneously
multiply the coefficients in the second row of the matrix by −1.

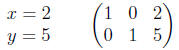
We can read off the solution to the system from the matrix as well as
from the equations.

Elementary Row Operations on Matrices

The three elementary operations we earlier stated for systems of
linear equations translate as follows to elementary row operations on
matrices.

• Multiply a row by a non-zero constant. By this, we really mean
to multiply every element of a row by the same non-zero constant.
We can also divide a row by a non-zero constant, since
division is a form of multiplication.
• Add a multiple of one row to another. By this, we really mean
to take a multiple of each element of one row and add it to the
corresponding element of another row. We can also subtract a
multiple of one row from another, since subtraction is a form of
addition.
• Interchange two rows.

Matrices - Terminology and Notation

A matrix is simply a rectangular array of numbers. It corresponds
to a two-dimensional array in just about any computer language. A
spreadsheet can be viewed as a large matrix. Newspapers make extensive
use of matrices, from box scores and standings in the sports pages
to the stock listings in the financial section.

A matrix has rows and columns; the rows go across, from left to right
and the columns go vertically, up and down.

We often refer to a matrix via a capital letter, such as A, and we may
write A_r×c to indicate the matrix has r rows and c columns.

The entry in the i^th row and j^th column of a matrix A is referred to as
a_i,j , and we sometimes write A = (a_i,j).

A matrix is generally enclosed in a large pair of parentheses.

The Augmented Matrix

Every system of linear equations has a corresponding augmented matrix.
We get the augmented matrix by writing down the coefficients of
each equation in order in a row and then writing the constant from the
write side of the equation at the end of the row. Be careful that zero
coefficients are included.

A system of m equations with n unknowns will yield an m × n + 1
matrix, that is, a matrix with m rows and n + 1 columns.

Pivoting

A key process both in solving systems of equations and in solving
linear programming problems using the Simplex Method is called pivoting.
We pivot about a given entry in a given row and column. Pivoting
is a two-step process, hence the term.

Suppose we wish to pivot about the entry in the i^th row, jth column.
• Step 1: Divide the i^th row by a_i,j, the entry in the i^th row, j^th
column. The gives a new matrix with a 1 in the i^th row, j^th
column.
• Step 2: For every other row, let k be the element in the j^th
column of that row. Subtract k times the i^th row from that
row. That will put a 0 in every row in the j^th column except
for the i^th row.

Example

Pivot about the second row, third column of the matrix

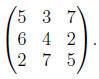
Step 1: Divide the second row by 2 to get:

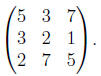
Step 2: First subtract 7 times the second row from the first row to get:

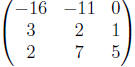and then subtract 5 times the second row from the

third row to get:

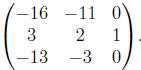
Gaussian Elimination

The method of Gaussian Elimination amounts to repeatedly applying
the Pivot Method to the augmented matrix of a system of equations
until the solution is obvious.

• We start by pivoting about the entry in the first row, first column.
If the entry in that place is 0, we first interchange the first
row with another row with a non-zero entry in the first column
and then pivot.
• After we pivot about a given row and column, we go down one
row and to the right one column and pivot about that entry if
it’s not 0. If that entry is 0, we first interchange that row with
some row below it with a non-zero entry in that column and
then pivot. If there is no non-zero entry further down in that
column, we go over one row to the right and try to pivot there.
• We continue until we reach the lower right hand corner.