Systems of Linear Equations and Problem
Solving
SOLVING SYSTEMS OF EQUATIONS GRAPHICALLY
We can use the Intersection feature from the Math menu on
the Graph screen of the TI-89 to solve a system of two equations
in two variables.
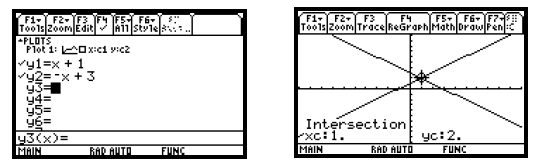
Section 8.1, Example 4(a) Solve graphically:
y − x = 1,
y + x = 3.
We graph the equations in the same viewing window and then
find the coordinates of the point of intersection. Remember that
equations must be entered in “y =” form on the equation-editor screen, so we
solve both equations for y. We have y = x + 1 and
y = −x + 3. Enter these equations, graph them in the standard viewing window,
and find their point of intersection as described
on page 131 of this manual. We see that the solution of the system of equations
is (1, 2).
MODELS
Sometimes we model two situations with linear functions and then want to find
the point of intersection of their graphs.
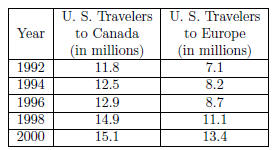
Section 8.1, Example 6 (d), (e) The numbers of U. S. travelers to Canada
and to Europe are listed in the following table.
(d) Use linear regression to find two linear equations
that can be used to estimate the number of U. S. travelers to Canada and
Europe, in millions, x years after 1990.
(e) Use the equations found in part (d) to estimate the
year in which the number of U. S. travelers to Europe will be the same
as the number of U. S. travelers to Canada.
(d) Enter the data in the Data/Matrix editor as described
on page136 of this manual. We will express the years as the number
of years since 1990 (in other words, 1990 is year 0) and enter them in c1. Then
enter the number of U. S. travelers to Canada, in
millions, in c2 and the number of U. S. travelers to Europe, in millions, in c3.

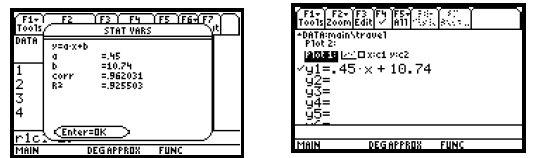
Now use linear regression to fit a linear function to the
data in c1 and c2. The function should also be copied to the equationeditor
screen. We will copy it as y1. See page 137 of this manual for the procedure to
follow. We get y1 = 0.45x + 10.74.
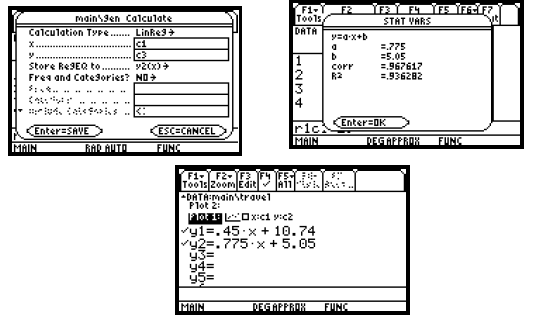
Next we fit a linear function to the data in c1 and c3,
enteringc1 as x and c3 as y on the Calculate screen. This function will
be copied to the equation-editor screen as y2. To enter c3 as y, position the
blinkingcursor in the y box and press  3. 3.
To select y2 as the function to which the regression equation will be copied,
position the cursor beside “Store Reg EQ to,” press

, use the  key to highlight y2(x) and press key to highlight y2(x) and press
 . We get y2 = 0.775x + 5.05. . We get y2 = 0.775x + 5.05.
(e) To estimate the year in which the number of U. S.
travelers to Europe will be the same as the number of U. S. travelers to
Canada, we solve the system of equations
y = 0.45x + 10.74,
y = 0.775x + 5.05.
We graph the equations in the same viewing window and then
use the Intersection feature to find their point of intersection.
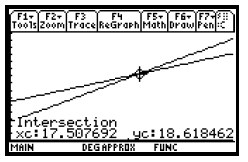
Through a trial-and-error process we find that [0, 30, 0, 30], xscl = 2, yscl =
2, provides a good window in which to see this point.
We see that the solution of the system of equations is approximately (17.51,
18.62), so the number of U. S. travelers to Europe
will be the same as the number of U. S. travelers to Canada about 17.5 years
after 1990, or in 2008.
ELIMINATION USING MATRICES
Matrices with up to 999 rows and 99 columns can be entered
on the TI-89. The row-equivalent operations necessary to write a
matrix in row-echelon form or reduced row-echelon form can be performed on the
calculator, or we can go directly to row-echelon
form or reduced row-echelon form with a single command. We will illustrate the
direct approach for finding reduced row-echelon
form.
Section 8.6, Example 1 Solve the following system
using a graphing calculator:
2x + 5y − 8z = 7,
3x + 4y − 3z = 8,
5y − 2x = 9.
First we rewrite the third equation in the form ax + by +
cz = d:
2x + 5y − 8z = 7,
3x + 4y − 3z = 8,
−2x + 5y = 9.
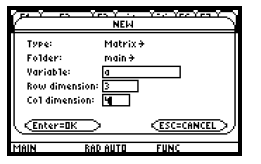
Then we enter the coefficient matrix
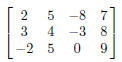
in the Data/Matrix editor. We will call the Matrix a.
Press 
to go to the Data/Matrix editor and set up a matrix named A with 3 rows and 4
columns. If a matrix named a has previously
been saved in your calculator, an error message will be displayed. If this
happens, you can select a different name for the matrix we are about to enter or
you can delete the current matrix a and then enter the new matrix as a. To
delete a matrix press 
 to highlight the name of the matrix being
deleted, and then press to highlight the name of the matrix being
deleted, and then press  (VAR-LINK is the (VAR-LINK is the
second operation associated with the  key.) key.)
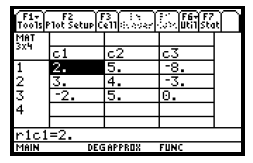
Enter the elements of the first row of the matrix by
pressing 2  The cursor The cursor
moves to the element in the second row and first column of the matrix. Enter the
elements of the second and third rows of the
augmented matrix by typing each in turn followed by
 as above. Note that the screen only displays
three columns of as above. Note that the screen only displays
three columns of
the matrix. The arrow keys can be used to move the cursor to any element at any
time.
Matrix operations are performed on the home screen and are
found on the Math Matrix menu. Press 
to leave the matrix editor and go to this screen. Access the Math Matrix menu by
pressing  4. (MATH is the 4. (MATH is the
second operation associated with the 5 numeric key.) The reduced row-echelon
form command is item 4 on this menu. Copy it to
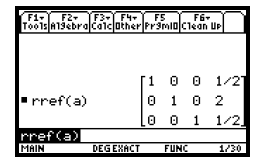
the entry line of the home screen by pressing4. We see the command “rref(” on
the entry line.
Since we want to find reduced row-echelon form for matrix
a, we enter a by pressing  Finally press Finally press
 to to
see reduced row echelon form of the original matrix. We see that the solution of
the system of equations is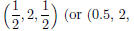 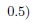 if
Auto or Approximate mode is selected rather than Exact mode). if
Auto or Approximate mode is selected rather than Exact mode).
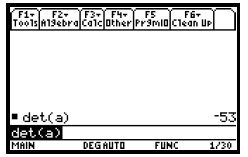
EVALUATING DETERMINANTS
We can evaluate determinants using the “det” operation from the MATRIX MATH
menu.
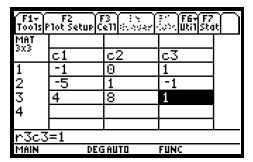
Section 8.7, Example 3 Evaluate:
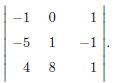
First enter the 3 x 3 matrix
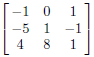
as described on pages 151 and 152 of this manual. We will
enter it as matrix a.
Then press  to go to
the home screen. Next press to go to
the home screen. Next press  4 to access the
Math Matrix menu. 4 to access the
Math Matrix menu.
Press 2 to copy the “det(” operation to the entry line of the home screen. Then
enter the matrix name a by pressing  Finally, press
Finally, press  to find the value of the
determinant of matrix a. to find the value of the
determinant of matrix a.
INEQUALITIES IN TWO VARIABLES
The solution set of an inequality in two variables can be
graphed on the TI-89.
Section 8.9, Example 4 Use a graphing calculator to
graph the inequality 8x + 3y > 24.
First we write the related equation, 8x + 3y = 24, and solve it for y. We g et
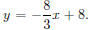 We will enter this as y1. Press We will enter this as y1. Press

 to go to the
equation-editor screen. If there is currently an entry for y1, clear it. Also
clear or deselect any other equations to go to the
equation-editor screen. If there is currently an entry for y1, clear it. Also
clear or deselect any other equations
that are entered. Now enter 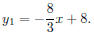 Since the
inequality states that 8x + 3y > 24, or y is greater than Since the
inequality states that 8x + 3y > 24, or y is greater than
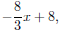 , we want , we want
to shade the half-plane above the graph of y1. To do this, use the cursor to
highlight y1. Then press  to display the
Style menu. Choose item 7, Above, by pressing7. (To shade below a line we would
press 8 to select Below.) Then press to display the
Style menu. Choose item 7, Above, by pressing7. (To shade below a line we would
press 8 to select Below.) Then press  6 6
to see the graph of the inequality in the standard viewing window.
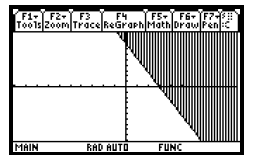
Note that when the “shade above” Style is selected it is
not also possible to select the “Dot” style so we must keep in mind the
fact that the line 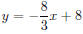 is not included in the
graph of the inequality. If you graphed this inequality by hand, you would is not included in the
graph of the inequality. If you graphed this inequality by hand, you would
draw a dashed line.
SYSTEMS OF LINEAR INEQUALITIES
We can graph systems of inequalities by shading the
solution set of each inequality in the system with a different pattern. When
the “shade above” or “shade below” style options are selected the calculator
rotates through four shading patterns. Vertical lines
shade the first function, horizontal lines the second, negatively sloping
diagonal lines the third, and positively sloping diagonal
lines the fourth. These patterns repeat if more than four functions are graphed.
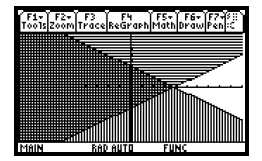
Section 8.9, Example 8 Graph the system
x + y ≤ 4,
x −y < 4.
First graph the equation x+y = 4, enteringit in the form y
= −x+4. We determine that the solution set of x+y ≤ 4 consists
of all points on or below the line x + y = 4, or y = −x + 4, so we select the
“shade below” style for this function. Next graph
x − y = 4, enteringit in the form y = x − 4. The solution set of x −y < 4 is all
points above the line x − y = 4, or y = x − 4, so
for this function we choose the “shade above” style. (See Example 4 above for
instructions on selectingst yles.) Now press  6
6
to display the solution sets of each inequality in the system and the region
where they overlap in the standard viewing window.
The region of overlap is the solution set of the system of inequalities. Keep in
mine that the line x+y = 4, or y = −x+4, is part
of the solution set while x − y = 4, or y = x − 4, is not.
|