Solving Quadratic Equations by Factoring

Questions

1. Solve x² − x − 20 = 0.
2. Solve x² + 11x + 18 = 0.
3. Solve 8x² = 72.
4. Solve (x − 5)(x + 4) = 2(x − 5).
5. Solve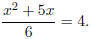

6. Solve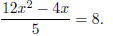

7. The area of a rectangular garden is 140 square meters. The width is 3 meters longer than one-half of the length. Find
the length and width of the garden.

8. Jules is standing on a platform 6 meters high and throws a ball straight up as high as he can at a velocity of 13 meters
per second. At what time t will the ball hit the ground? How far from the ground is the ball 2 seconds after Jules threw
the ball (assume the ball is 6 meters from the ground when it leaves Jules’ hand).

Solutions

1.

x2 − x − 20 = 0	Find two numbers product is −20 and sum is −1: −5, 4.
(x − 5)(x + 4) = 0	Use Zero Factor Property.
(x − 5) = 0 or (x + 4) = 0	Solve each linear equation.
x = 5 or x = −4

Check:
(5)² − (5) − 20 = 25 − 25 = 0
(−4)² − (−4) − 20 = 16 − 16 = 0

2.

x2 + 11x + 18 = 0	Find two numbers product is 18 and sum is 11: 2, 9.
(x + 2)(x + 9) = 0
(x + 2) = 0 or (x + 9) = 0
x = −2 or x = −9

Check:
(−2)² + 11(−2) + 18 = 4 − 22 + 18 = 0
(−9)² + 11(−9) + 18 = 81 − 99 + 18 = 0

3.

8x2 − 72 = 0	Factor.
8(x2 − 9) = 0	Factor.
x2 − 9 = 0	Divide by 8. Difference of Squares.
(x + 3)(x − 3) = 0 (x + 3) = 0 or (x − 3) = 0 x = −3 or x = 3

Check:
8(−3)² = 8(9) = 72
8(3)² = 8(9) = 72

Alternate solution, which only works because there was no x term:

8x2 = 72
x2 = 9
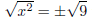	when taking square root of both sides of equation, one side can be ±.
x = ±3

4. Start by multiplying everything to get in form ax² + bx + c = 0.

(x − 5)(x + 4) = 2(x − 5)
x² − x − 20 = 2x − 10
x² − x − 20 − 2x + 10 = 0
x² − 3x − 10 = 0 Find two numbers product is −10 and sum is −3: −5, 2.
(x − 5)(x + 2) = 0
(x − 5) = 0 or (x + 2) = 0
x = 5 or x = −2

Check:
((5) − 5)((5) + 4) − 2((5) − 5) = 0
((−2) − 5)((−2) + 4) − 2((−2) − 5) = −14 + 14 = 0

5. Start by multiplying everything to get in form ax² + bx + c = 0.

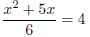
x² + 5x = 24
x² + 5x − 24 = 0 Find two numbers product is −24 and sum is 5: 8,−3.
(x + 8)(x − 3) = 0
(x + 8) = 0 or (x − 3) = 0
x = −8 or x = 3

Check:

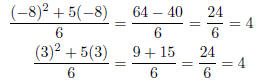
6. Start by multiplying everything to get in form ax² + bx + c = 0.

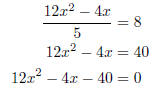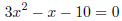	Grouping Method: Find two numbers product is −30 and sum is −1: −6, 5.
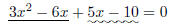	Factor by grouping.

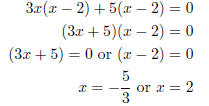Check:

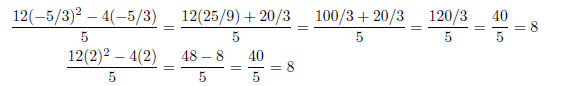
7. Let x be the length (in meters). Then the width is x/2 + 3 meters. Area is 140 m².

Area = (length)(width)

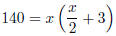
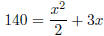write in form ax² + bx + c = 0.

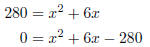
x² + 6x − 280 = 0 Find two numbers product is 6 and sum is −280: −14, 20.
(x − 14)(x + 20) = 0
(x − 14) = 0 or (x + 20) = 0
x = 14 or x = −20

Exclude the x = −20 as unphysical (can’t have negative length). So The length is x = 14 meters. Width is 10 meters.

8. Set h = 6 and v = 13 in our model equation S = −5t² + vt + h (see handout).

5t² + 13t + 6 = 0 Ball hits ground when S = 0. Use Grouping Method to factor.
−5t² + 13t + 6 = 0 Find two numbers product is −30 and sum is 13: 15,−2.
−5t² + 15t − 2t + 6 = 0
−5t(t − 3) − 2(t − 3) = 0
(−5t − 2)(t − 3) = 0
(−5t − 2) = 0 or (t − 3) = 0
t = −2/5 or t = 3

Exclude the t = −5/3 as unphysical, so the ball hits the ground after 3 seconds.

Two second after throwing the ball, it it S = −5(2)² + 13(2) + 6 = −20 + 26 + 6 = 12 meters above the ground.