Solving Equations
Recall that the solution of an equation is a number
that, when substituted for the variable,
results in a true equation. To solve an equation means to find all of the
solutions of the
equation. We have found the solution to an equation when we reduce the equation
to the
form variable term = constant, where the coefficient on the variable term
is positive one.
We can use arithmetic to help us determine the solution to
a linear equation using the
following principles of equations.
The addition principle of equations states that if
we add the same number to both sides
of the equation we do not change the solution of the equation. In other words,
if a = b is
true, then a + c = b + c is also true.
When using the addition principle, we often say that we
“add the same number to both
sides of an equation.” We can also “subtract the same number from both sides of
an
equation,” since subtraction can be regarded as adding the opposite. This fact
leads to the
following principle.
The subtraction principle of equations states that
if we subtract the same
number from both sides of the equation we do not change the solution of the
equation. In other words, if a = b is true, then a − c = b − c is also true.
The multiplication principle of equations states
that if we multiply both sides of the
equation with the same number (except for zero) we do not change the solution of
the
equation. In other words, if a = b is true, then a × c = b × c is also true when
c ≠ 0 .
When using the multiplication principle, we often say that
we “multiply both sides of the
equation by the same number.” We can also “divide both sides of the equation by
the
same number,” since division can be regarded as multiplying by the reciprocal.
This fact
leads to the following principle.
The division principle of equations states that if
we divide both sides of the
equation with the same number (except for zero) we do not change the solution of
the equation. In other words, if a = b is true, then a ÷ c = b ÷ c is also true
when
c ≠ 0 .
Section 2.2 Using the Principles Together
When the terms in an equation contain numerical coefficients that are
fractions or
decimals, the difficulty in solving the equation is often increased. However, we
can “clear
the equation of fractions or decimals” by applying the multiplication principle
as follows.
To clear an equation of fractions, multiply every term in
the equation by the least
common denominator of the fractional coefficients.
To clear an equation of decimals, multiply every term in
the equation by 10n,
where n is the most number of decimal places on any coefficient in the equation.
When solving equations, we often need to use more than one
principle. However, the
order that we use these principles is important. The following procedure
provides an
accurate method for solving linear equations.
An Equation-Solving Procedure
1. Use the multiplication principle to clear any fractions or decimals in
the equation.
(This step is optional, but can ease computations.)
2. If necessary, use the distributive law to remove parentheses on each side of
the
equal symbol. Then simplify each side of the equation by combining the like
terms on each side.
3. Use the addition or subtraction principle, as needed, to get all variable
terms on
one side of the equation and all of the constant terms on the other side of the
equation.
4. Combine like terms on both sides of the equation again, if necessary.
5. Use the multiplication or division principle to reduce the coefficient on the
variable term to positive one.
6. Check your solution by substituting it back into the equation to see if it
produces a
true equation.
Section 2.3 Formulas
A formula is an equation that represents the relationship between two
or more quantities.
They have letters that represent quantities that can vary, but they may also
have letters
that represents constants.
If we are given the values(s) for all but one of the
variable term(s) we can evaluate any
formula for the remaining variable term by substituting the known values into
the
equation and solving for the remaining term.
Sometimes, we need to “rearrange” the terms in a formula.
This “rearrangement” is
called solving for a letter in the formula. For example, let’s say that we want
to solve for
the letter x in a formula. We want to rearrange the formula to be in form x =
expression,
where the expression on the right-hand side of the equation is obtained from the
rearrangement of the original formula and does not contain the variable x.
We have a procedure we can follow to solve for a letter in
a formula. It is outlined below.
To Solve a Formula for a Given Letter
1. If the letter for which you are solving appears in a fraction, use the
multiplication
principle to clear fractions.
2. Get all terms with the letter for which you are solving on one side of the
equation and
all other terms on the other side using the addition and/or subtraction
principle.
3. Combine like terms, if possible. If the terms containing the variable you are
solving
for are not like terms, you must factor the expression containing the variable
of
interest.
4. Multiply or divide by the coefficient of the variable of interest to reduce
its
coefficient to positive one.
Notice that the steps above are similar to those used in
Section 2.2 to solve equations.
The main difference is the possible necessity of factoring in step 3.
Section 2.4 Applications with Percent
The percent symbol, %, means “per hundred.” Hence, “n parts per hundred” is
denoted as
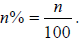
For problem solving with percents, it is a necessary skill
to be able to convert from
percent notation to decimal notation and vice versa.
• To convert from percent notation to decimal notation,
move the decimal point two
places to the left and drop the percent symbol.
• To convert from decimal notation to percent notation, move the decimal point
two
places to the right and write a percent symbol.
Solving Percent Problems
There are many real world situations that involve the use of percent. We can
solve many
problems representing these situations through the use of the basic percent
equation.
The Basic Percent Equation: Percent · base =
amount, where the percent is in decimal
notation and the base is the original quantity we are finding the percentage of.
Percent increase is used to represent how much a
quantity has increased over its original
value. There are many real world applications of percent increase.
A basic equation can be used to solve these types of
problems.
Basic Percent Increase Equation: (1+ r)base =
amount
where r represents the percent increase in decimal notation,
the base represents the original value, and
the amount is the quantity that the original value increased to.
Percent decrease is used to represent how much a
quantity has decreased from its
original value. There are many real world applications of percent decrease.
A basic equation can be used to solve these types of
problems.
Basic Percent Decrease Equation: (1− r)base =
amount
where r represents the percent decrease in decimal
notation,
the base represents the original value, and
the amount is the quantity that the original value decreased to.
Section 2.5 Problem Solving
The goal of every mathematics course is to develop problem
solving skills. There are
some steps one can take to make problem solving easier or more manageable.
Five Steps for Problem Solving in Algebra
1. Familiarize yourself with the problem.
2. Translate to mathematical language. This often means writing an equation.
3. Carry out some mathematical manipulation. This often means solving an
equation.
4. Check your possible answer in the original problem.
5. State the answer clearly.
Of these five steps the hardest to implement is the first
one. The following list gives some
hints on how to get started with step one.
To Become Familiar with a Problem
1. Read the problem carefully. Try to visualize the problem.
2. Reread the problem, perhaps aloud. Make sure you understand all important
words.
3. List the information given and the question(s) to be answered. Choose a
variable
(or variables) to represent the unknown and specify what the variable
represents.
4. Look for similarities between the problem and other problems you have already
solved.
5. Find more information. Look up a formula in a book, at a library, or on-line.
Consult a reference librarian or an expert in the field.
6. Make a table that uses all the information you have available. Look for
patterns
that may help in the translation.
7. Make a drawing and label it with known and unknown information, using
specific
units if given.
8. Think of a possible answer and check the guess. Observe the manner in which
the
guess is checked.
Section 2.6 Solving Inequalities
A linear inequality in one variable is a mathematical statement that states
that one
expression is either less than, less than or equal to, greater than, or greater
than or equal
to another expression.
Linear inequalities may be true or false. A solution of a
linear inequality is a value of the
variable which makes the inequality true.
There are many ways to describe the solutions to an
inequality. Three common methods
are:
1. Inequality notation – x < c, x ≤ c, x > c, x ≥ c
2. Graphing them on a real number line, or
3. Set- builder notation – For example: {x| x < c} and reads “the set of all x
such
that x < c .
Given an inequality of the form x < c or x ≤ c, we say
that the constant c is an upper
bound of the solution set. For x < c, the upper bound c is not included
in the solution set.
For x ≤ c, the upper bound c is included in the solution set.
Given an inequality of the form x > c or x ≥ c, we say
that the constant c is a lower
bound of the solution set. For x > c, the lower bound c is not included
in the solution set.
For x ≥ c, the lower bound c is included in the solution set.
To graph the solution set of a linear inequality in the
form x < c, x > c, x ≤ c, or x ≥ c on
a number line:
• Plot the upper or lower bound, c, of the inequality on
the number line.
o Use an open dot if the bound is not included in the solution set.
o Use a closed dot if the bound is included in the solution set.
• Complete the graph using a solid line.
o Cover all points to the left of the upper bound for a “less than” or “less
than or equal to” inequality.
o Cover all points to the right of the lower bound for a “greater than” or
“greater than or equal to” inequality.
Solving Inequalities
We can solve any inequality so that it is in the form x < c, x > c, x ≤ c,
or x ≥ c.
Addition Property of Inequalities
Given expressions a, b, and c,
If a < b , then a + c < b + c .
If a > b , then a + c > b + c .
If a ≤ b , then a + c ≤ b + c .
If a ≥ b , then a + c ≥ b + c .
This property holds for subtraction as well, because subtraction is defined as
adding the
opposite of a number.
Multiplication Property of Inequalities
Given expressions a, b, and c with c > 0 (c is positive),
If a < b , then ac < bc .
If a > b , then ac > bc .
If a ≤ b , then ac ≤ bc .
If a ≥ b , then ac ≥ bc .
Given expressions a, b, and c with c < 0 (c is negative),
If a < b , then ac > bc .
If a > b , then ac < bc .
If a ≤ b , then ac ≥ bc .
If a ≥ b , then ac ≤ bc .
This property holds true for division as well, because division is defined as
multiplying
by the reciprocal of a number.
SUMMARY
To solve a linear inequality algebraically, use the same methods you did when
solving a
linear equation. The exception being if you need to multiply or divide by a
negative
number, reverse the sign of the inequality.
Section 2.7 Solving Applications with Inequalities
To solve word problems with inequalities, we need to be
able to translate the words into
the correct inequality symbol. The following table represents the most common
phrases
and how they should be translated.
| Important Word Phrase |
Inequality Symbol |
| is at least |
≥ |
| is at most |
≤ |
| cannot exceed |
≤ |
| must exceed |
> |
| is less than |
< |
| is more than |
> |
| no more than |
≤ |
| no less than |
≥ |
| is between |
? depends… |
|